Gerilim Düşümü

Gerilimde bir düşme olmasa ne güzel olurdu. İncecik kablolarla kaynağın gerilimini istediğimiz kadar uzağa taşır, en ufak bir enerji kaybı da yaşamazdık.  Ama maalesef böyle bir dünya yok. En azından süper iletken teknolojisi ilerleyene kadar bu gerilim düşümü hesaplarını yapmaya devam etmek zorundayız.

Bildiğiniz gibi bir gerilim kaynağını, bir tüketece iletkenle bağlarız. İletkenler de neticede bir öz empedans içerirler ve tüketecin ihtiyacı olan akım iletkenden geçerken öz empedansları oranında enerjiyi kullanırlar. Isı ve manyetik alan oluşturmak için kullandıkları bu enerji  kimsenin işine yaramadığı için kayıp enerjidir. Durum böyle olunca kablo tip ve kesit  seçiminde bu kaybolan bu enerjinin minimum olması kriteri göz önüne alınır.

Mevzuatımızda Gerilim Düşümü

Elektrik İç Tesisleri Yönetmeliği Madde 57’de “İletken ve kabloları boyutlandırılması” başlıklı bir kısım vardır. Analaşılacağı üzer bu kısımda kabloların nasıl boyutlandırılacağı madde madde belirtilmiştir. Bu maddelerin 3.sünde gerilim düşümü anlatılmaktadır.

Yönetmelikte şu ifadeler vardır:

i) İç tesis hatlarında sürekli en büyük işletme akımı ile işletme gerilimine göre yüzde gerilim düşümü,

Yapı bağlantı kutusu ile tüketim araçları arasında, aydınlatma ve priz devreleri için % l,5’i, motor devreler için % 3 ‘ü, geçmemelidir.

ii) Yapının yada yapı kümesinin beslenmesi için bir transformatör kullanılmışsa, bu transformatörü çıkış uçları ile yapı bağlantı kutusu arasındaki gerilim düşümü % 5’i geçmemelidir. (Açıklama : Gerilim düşümü hesapları, gerekli görüldüğünde görünen güç göz önüne alınarak yapılmalıdır.)

Bu durumda, kendi trafosu bulunan tesislerde toplam gerilim düşümü, aydınlatma ve priz devreleri için %6,5, motor devreleri için %8 olabilir, sonucu çıkmaktadır.

İkinci maddeye bir açıklama ifadesi eklenip, gerekli görüldüğünde görünen güç göz önüne alınarak hesap yapılması gerektiği vurgulanmıştır ama o gerekli haller anlatılmamıştır. Görünür güce atıfta bulunulduğuna göre X, yani reaktans değeri aklımıza gelmelidir. Yani devremizdeki  reaktans değeri yüksekse (ki bu daha çok büyük kesitli ana besleme kablolarında ve orta gerilim şebekelerinde dikkate alınması gereken noktalara ulaşır) gerilim düşümü hesaplarında reaktansı da ihmal etmeden işlemler sokmalıyız.

iii) Elektrik iç tesislerinde gerilim düşümlerini hesaplanmasında aşağıdaki formüller kullanılabilir:

-Bir fazlı alternatif akım tesislerinde:
Akım biliniyorsa : u = 2 L. I.cosp / X.S
Güç biliniyorsa : u = 2 L. N / X. S. U.
Yada yüzde gerilim düşümü olarak : % e =2 . 100 .L . N / X . S .U2

-Üç fazlı dengeli yüklü alternatif akım tesislerinde :
Akım şiddeti biliniyorsa : e = l,73 L. I.cos p / X.S
Güç biliniyorsa : e = L.N / X .S. U yada % e = 100. L. N/ X .S U

Yukarıdaki formüllerde

e: Gerilim düşümü (Volt)
(Bir fazlı hatlarda gidişi ve dönüş iletkenleri üzerindeki; üç fazlı hatlarda ise yalnızca faz iletkeninin üzerinde gerilim düşümü hesaplanacaktır.)
L: Hat uzunluğu (metre)
I: Akım şiddeti (amper)
U: İşletme gerilimi (üç fazlı şebekelerde faz arası gerilimi) (volt)
Cosp : güç katsayısı (omik yüklenmede ve doğru akımda cosp=1 alınır)
N: Güç (Watt)
X:Özgül iletkenlik katsayısı (m/ohm.mm2)-bakır için = 50 m/ohm.mm2 alınır)
S : İletken kesiti (mm2)

Açıkçası, gerilim düşümü ile ilgili yönetmeliğimizdeki bu formüllerin oldukça sığ olduğunu düşünüyorum.Belki bilgisayar destekli proje hazırlama imkanlarının olmadığı eski dönemlerde bazı hesapları ampirikleştirmek işleri kolaylaştırabilirdi ama günümüzde hala eski metotlarda ısrar etmek anlaşılır gibi değil. Bugün, tüm dünyanın otorite kabul ettiği IEEE’nin yayınlarını incelediğimizde artık gerilim düşümünün tam değerini veren formüllerin kullanıldığı görülmektedir.

Bu noktada, “tam değer mi?” diye sorabilirsiniz. Açıkçası, bugüne kadar yapılan gerilim düşümü hesapları belli bir hata payı içinde kalmak suretiyle yaklaşık olarak hesaplanmaktaydı.  Hatta bazı hesaplarda iletken reaktans değerlerini ihmal etmekle bu hata payı daha da artmaktaydı.

Gerilim Düşümü Teknik Tanımı

Burada linki verilen EMO yayınında, gerilim düşümü için şu tanım yapılmaktadır.

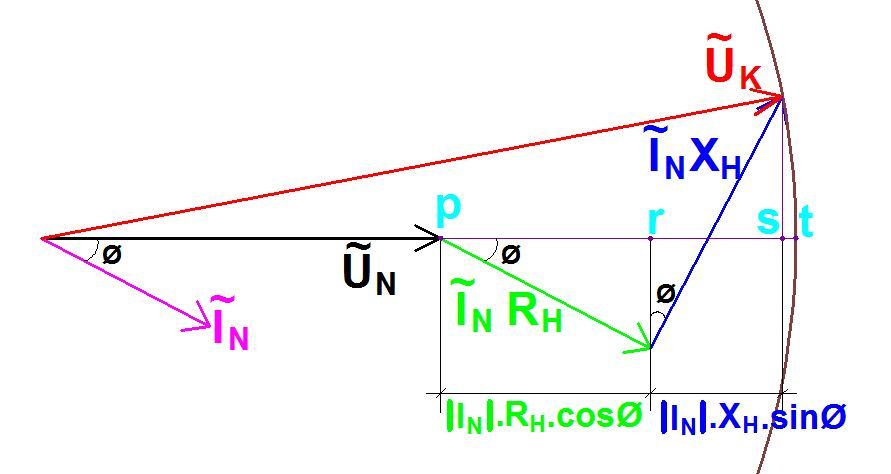
Bir hattın başındaki gerilim fazörü ile sonundaki gerilim fazörü arasındaki farka gerilim düşümü adı verilmektedir. Gerilim düşümü boyuna ve enine gerilim düşümleri olarak iki bileşenden oluşur. Alçak gerilim şebekelerinde boyuna gerilim düşümü etkin olup, enine gerilim düşümü dikkate alınmaz. Orta gerilim şebekelerinde gerilim düşümü hesaplarında her iki bileşen de hesaplanmalıdır. Boyuna gerilim düşümü ufak bir hata ile hattın başındaki gerilim fazörünün hat sonu gerilim fazörü üzerindeki izdüşümü ile hat sonu fazörü arasındaki fark gerilim olarak hesaplanır.

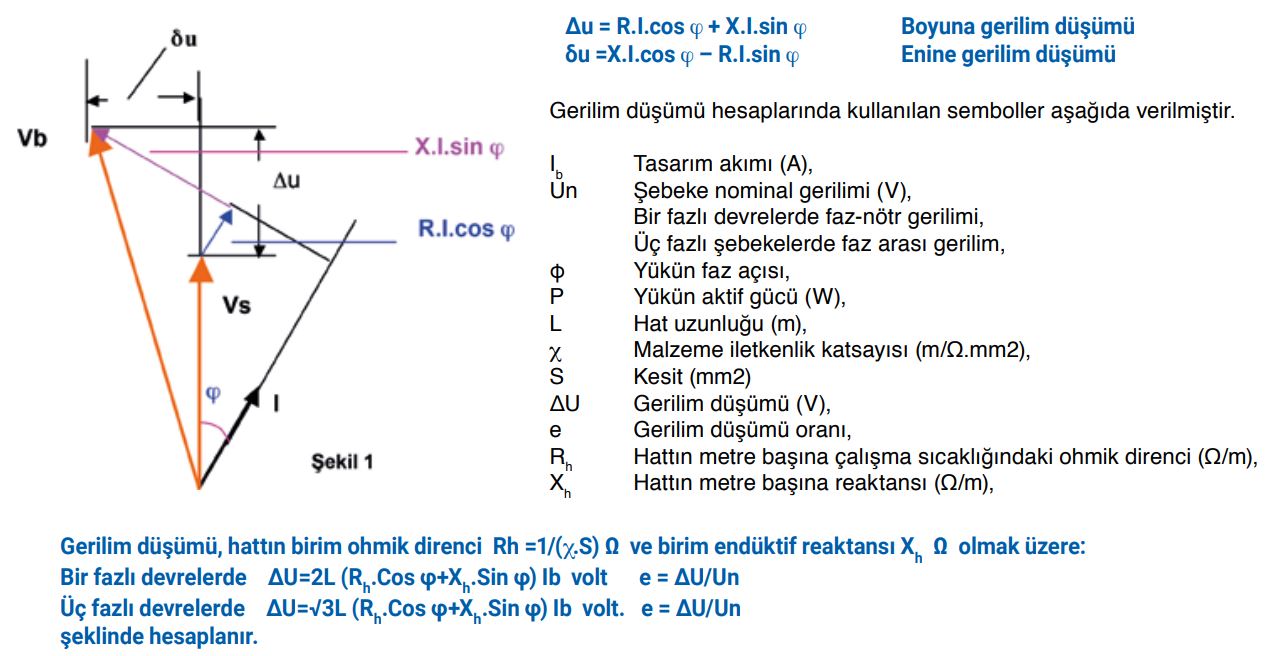
Yukarıda verilen tanım ve çizim gayet net olarak Gerilim Düşümü olayını anlatıyor ama konuyu biraz detaylandırmakta fayda var.

Aşağıda tekhat şeması verilmiş basit bir devre var. Bu devre bir panodan beslenen bir fazlı yük ve faz+nötr iletkeni bulunan bir besleme kablosundan oluşan basit bir devre.

Bu tekhat şeması verilen devreyi aşağıdaki şekilde genişletebiliriz.

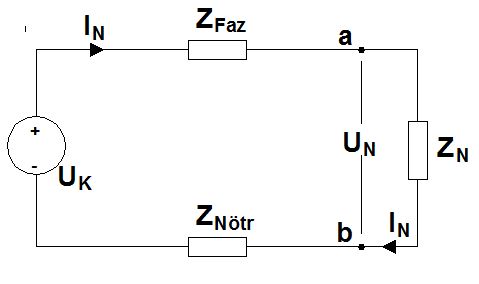
Burada verilen Z Faz, faz iletkenin empedansını, ZN yükün empedansını, Znötr ise nötr iletkeninin empedansını simgeliyor. Burada Zfaz ve Znötr birbirine eşittir ve toplanarak tek empedans( Z H) olarak ifade edilebilir. Bu durumda devremiz şu hale gelir.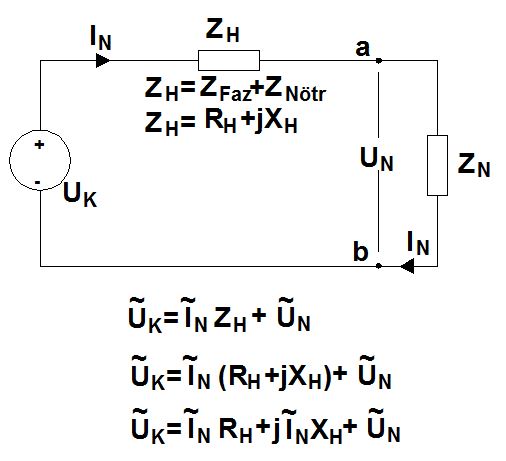

Burada, hat empedansının akımın şiddetine katkısı ihmal edilir. Çünkü devre akımını yükün akımı olarak kabul etmek yeterlidir, bu anlamda hat empedansı çok düşüktür. Elbette bu durum bir çelişki olarak algılanmamalıdır. Yani hem küçük deyip ihmal ediyoruz hem de gerilim düşümüne sebep olarak bu empedansı işaret ediyoruz. Unutmayalım ki,  hattan yük akımı geçtiğinde, ihmal ettiğimiz o küçük empedans gerilimi düşürmeye yetmektedir. Hattın empedansı akımı belirlerken ihmal edilir, gerilimi belirlerken dikkate alınır.

Dilenirse elbette hassas hesaplamalarla devre akımı, hat ve yük empedansları eklenip, kaynak gerilimine bölünerek tespit edilir ama çıkacak sonuç çok küçük bir farkla ihmal ettiğimiz durumun akım değerinden aşağıda olacaktır. Haliyle hat empedansını ihmal etmek hesaplamalara emniyetli tarafta kalmak anlamında katkı sağlamaktadır.

 

Yukarıda ulaştığımız denklemleri fazör bölgesinde ifade edersek, işimiz birkaç geometrik problem çözmeye kalır.

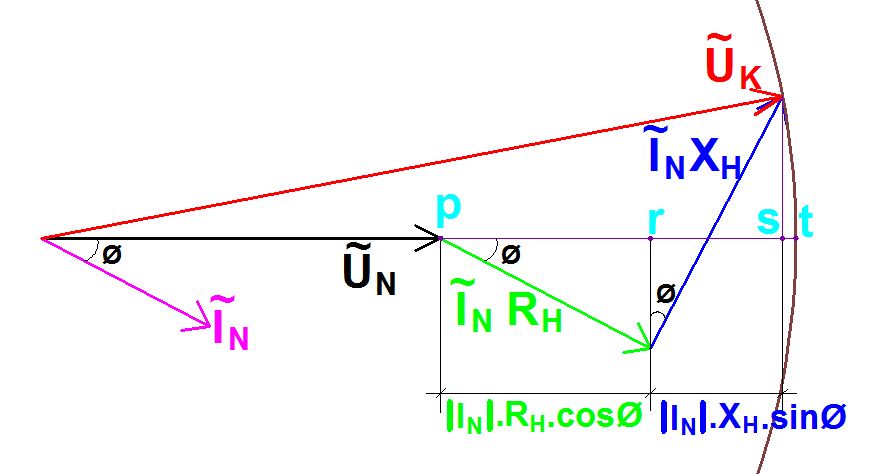
Bu resimdeki gerilim düşümü aslında p ve t noktaları arasındaki mesafedir. Ancak s ve t noktaları arası ihmal edilir ve gerilim düşümü olarak p ve s noktaları arası kabul edilir.

Yani p ve s noktaları arasındaki mesafe kadar gerilim kaynaktan yüke ulaşırken hat üzerinde kaybolmuştur. Geometrik bir takım çözümlemelerle p ve s noktaları arasındaki mesafeyi yani gerilim düşümünü şu şekilde bulabiliriz.

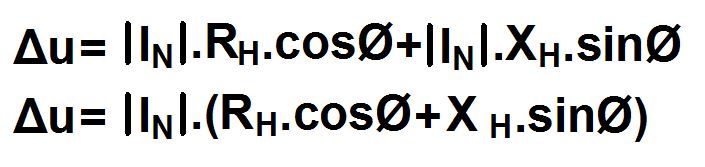
Ancak tekrar vurgulamak gerekirse, bu ifadede s ve t noktaları arasındaki mesafeyi ihmal ettik. Aslında bu mesafeyi hesaplamak zor sayılmaz. Sadece yukarıdaki gerilim düşümü formülümüze s ve t noktaları arasındaki mesafeyi verecek bir ifade daha eklenecek o kadar.

s ve t noktaları arasındaki mesafeyi hesaplamak için biraz geometri çalışalım:

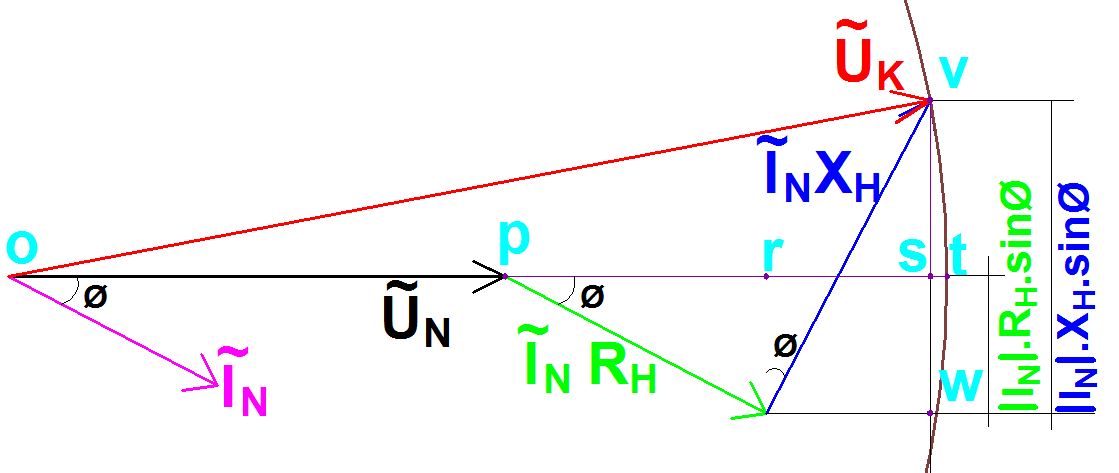
Yukarıdaki şekilde s  ve v noktaları arasındaki mesafeyi, w ve v arasındaki mesafeden s ve w noktaları arasındaki mesafeyi çıkararak bulabiliriz. Yani ¦sv¦=¦wv¦-¦sw¦

Böylece o, s ve v noktaları arasında bir dik üçgen oluştu. Bu dik üçgenin, o ve s noktaları arasındaki kenar uzunluğunu bulabiliriz.

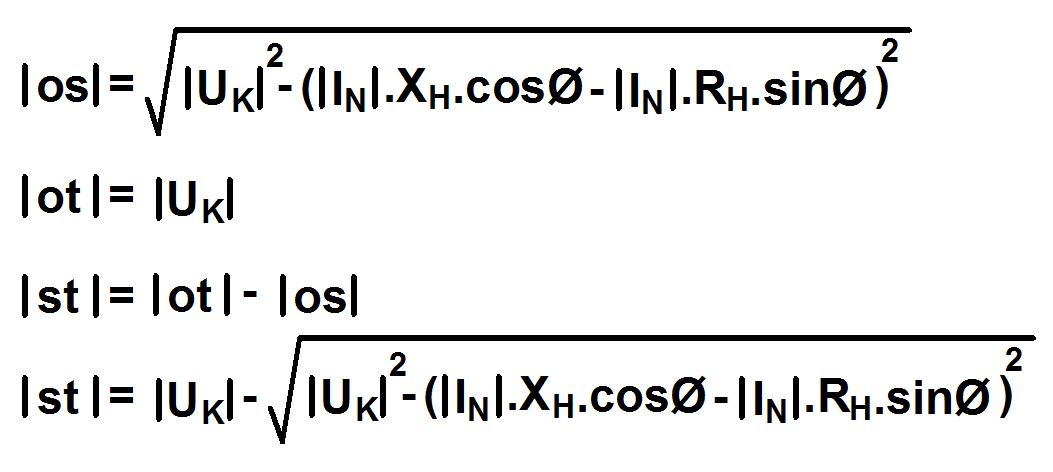
Böylece s ve t noktaları arasındaki mesafeyi de bulmuş olduk. Daha yukarıda bulduğumuz gerilim düşümü formülümüze bu değeri de ekleyerek hiç hata payı olmayan gerilim düşümü formülümüzü elde etmiş oluruz.

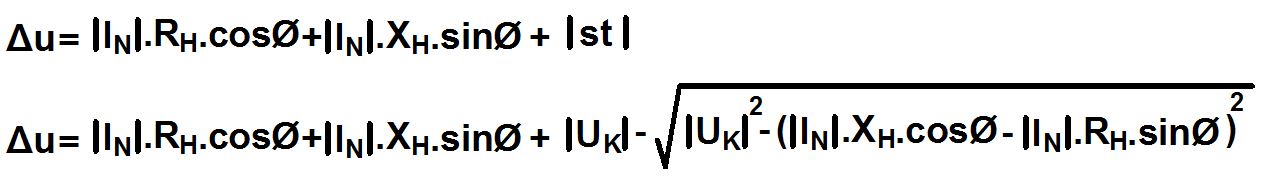
IEEE’nin yayınlarında (IEEE Standard 141) gerilim düşümü formülü olarak bu bulduğumuz ifade verilmektedir. Fakat açıkçası, hata payı dediğimiz kısım çok küçüktür. Bu nedenle ifademizi şu şekilde yazalım:

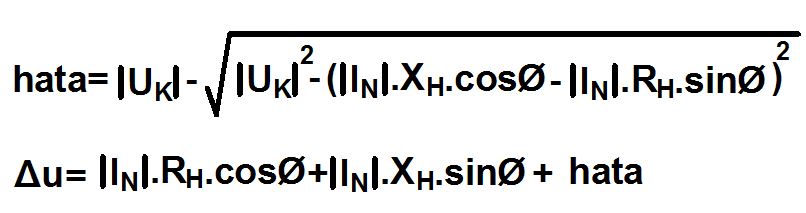
Gerilim düşümü hesaplarında ileri derece hassasiyet aranmıyorsa yani hesaplamalarımız kritik seviyelerde değilse veya bilgisayarda hesaplama programı yapılmıyorsa formülü karmaşıklaştırmaya hiç gerek yoktur. hata=0 kabul ederek ilk ulaştığımız formül gönül rahatlığıyla kullanılabilir.

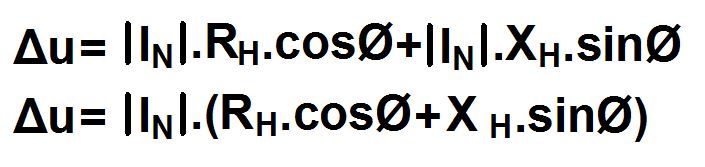
Hat empedansı

Bir işi yapmak için belirli bir şiddette akım çekmek zorundayız, haliyle gerilim düşümünü azaltacağız diye yük akımını azaltamayız. Yapacağımız tek şey yük akımını taşıdığımız iletkenin empedansını doğru seçmektir.

Empedansın iki bileşeni vardır: Direnç(R) ve reaktans (X)

Direnç (R)

SI ölçülerine göre, 1m uzunluğunda ve 1mm2 kesitindeki bir ilekenin, elektrik akımına karşı gösterdiği dirence özdirenç (ro) denir. Özdirenç değeri, malzemenin yapısından kaynaklanan ve o malzemeye özgü bir değerdir.

Alüminyum için  ro _Al = 0,028264 Ohm mm²/m ,bakır için  ro _Cu = 0,017857 Ohm mm²/m dir.

Özdirecin tersine iletkenlik denir. İletkenlik, Alüminyum için S_Al = 35,38 m/Ohm mm²  bakır için  S_Cu = 56 m/Ohm mm² dir.

Özdirenci, iletkenin L uzunluğu ile çarpıp S kesit değerine bölersek R direncini buluruz.

R= ro * L / S

Direnç ve Sıcaklık

Ancak vurgulamak gerekir ki direnç değeri sıcaklıkla değişir. Yukarıda verilen değerler 20ºC ortam sıcaklığındaki değerlerdir. İletken üzerinden akım geçip iletken ısındıkça direnç değeri artacaktır. Haliyle gerilim düşümü hesaplarında kablonun işletme sıcaklığındaki direnç değerlerini hesaba almak doğru olur.

Bir iletkenin T₁ sıcaklığındaki direnci R₁ olsun, sıcaklık biraz daha artıp T₂ sıcaklığına geldiğinde iletkenin direnci R₂ olacaktır.

Buna göre direncin sıcaklıkla değişimi aşağıdaki denkleme göre gerçekleşir

(R₂ – R₁) / R₁ = α (T₂ – T₁)  veya

R₂ = R₁ x [1 + α (T₂ – T₁) ]

α iletkenin direncinin sıcaklığa göre değişim katsayısıdır. Her maddenin kendine özgü bir değişim katsayısı bulunur. Bakır iletkenlerde  α =0,00393, alüminyum iletkenlerde α=0,00403 alınır.

Direnç ve Deri Etkisi ile Yakınlık Etkisi

Bir alternatif akım sisteminde gerilim düşümü hesabı yapıyorsak, hesaplaraa DC direnç değil AC direnci esas almak durumundayız. Kablo kataloglarında 20ºC sıcaklıkta DC direnç değerleri verilir. Halbuki işletme şartlarında bu direncin değerini arttıran başka faktörler oluşur. Alternatif akım sistemlerinde ortaya çıkan, deri etkisi ve yaklaşım etkisi denilen iki fenomen vardır. Bu iki etkinin sonuçlarının nasıl hesaplandığı IEC 60287-1-1 Part1-1 ‘de detaylı olarak anlatılmaktadır. Bu yazıda fazlaca detaya girilmeyecektir ancak bu iki etkiyi hesaba alarak kablo kesiti bazında 90ºC sıcaklıkta AC direnç karşılığını bulmak için aşağıdaki tabloyu kullanabiliriz.

Tablodan da görüleceği gibi AC direnç değerini kullanmak, küçük kesitli kablolarda pek önem arz etmese de özellikle büyük kesitli kablolarda önemli değişikliklere yol açmaktadır.

70ºC işletme sıcaklığına sahip kablolar için AC Direnç tablosu aşağıdadır. (Tablo-1)

Kesit	DC Direnç 20ºC	DC Direnç 70ºC	Deri Etkisi Katsayısı	Yaklaşım Etkisi Katsayısı	AC Direnç Katsayısı	AC Direnç 70ºC
mm2	Ohm/km	Ohm/km				Ohm/km
Bakır İletkenler (Yuvarlak Kesitli)
1,5	12,1	14,5	0,0000	0,0000	1,0000	14,5
2,5	7,41	8,87	0,0000	0,0000	1,0000	8,87
4	4,61	5,52	0,0000	0,0000	1,0000	5,52
6	3,08	3,69	0,0000	0,0000	1,0000	3,69
10	1,83	2,19	0,0000	0,0000	1,0000	2,19
16	1,15	1,38	0,0000	0,0000	1,0000	1,38
25	0,724	0,866	0,0001	0,0000	1,0001	0,866
35	0,524	0,627	0,0002	0,0000	1,0002	0,627
50	0,387	0,463	0,0004	0,0001	1,0005	0,463
70	0,268	0,321	0,0008	0,0006	1,0014	0,321
95	0,193	0,231	0,0015	0,0021	1,0037	0,232
120	0,153	0,183	0,0024	0,0054	1,0078	0,184
150	0,124	0,148	0,0037	0,0124	1,0161	0,151
185	0,0991	0,1186	0,0058	0,0299	1,0357	0,1228
240	0,0754	0,0902	0,0100	0,0847	1,0948	0,0988
300	0,0601	0,0719	0,0157	0,1887	1,2045	0,0866
400	0,0470	0,0562	0,0255	0,3948	1,4203	0,0799
500	0,0366	0,0438	0,0415	0,6817	1,7231	0,0755
600	0,0283	0,0339	0,0678	0,9645	2,0323	0,0688
Alüminyum İletkenler (Yuvarlak Kesitli)
2,5	12,22	14,69	0,0000	0,0000	1,0000	14,69
4	7,64	9,18	0,0000	0,0000	1,0000	9,18
6	5,09	6,12	0,0000	0,0000	1,0000	6,12
10	3,06	3,67	0,0000	0,0000	1,0000	3,67
16	1,91	2,29	0,0000	0,0000	1,0000	2,29
25	1,20	1,44	0,0000	0,0000	1,0000	1,44
35	0,868	1,043	0,0001	0,0000	1,0001	1,039
50	0,641	0,770	0,0001	0,0000	1,0001	0,767
70	0,443	0,532	0,0003	0,0000	1,0003	0,530
95	0,320	0,384	0,0006	0,0001	1,0007	0,383
120	0,253	0,304	0,0009	0,0003	1,0012	0,303
150	0,206	0,248	0,0014	0,0007	1,0020	0,247
185	0,164	0,197	0,0021	0,0017	1,0038	0,197
240	0,125	0,150	0,0037	0,0050	1,0086	0,151
300	0,100	0,120	0,0057	0,0120	1,0177	0,122
400	0,0778	0,0935	0,0094	0,0322	1,0416	0,0970
500	0,0605	0,0727	0,0155	0,0838	1,0993	0,0796

90ºC işletme sıcaklığına sahip kablolar için AC Direnç tablosu aşağıdadır. (Tablo-2)

Kesit	DC Direnç 20ºC	DC Direnç 90ºC	Deri Etkisi Katsayısı	Yaklaşım Etkisi Katsayısı	AC Direnç Katsayısı	AC Direnç 90ºC
mm2	Ohm/km	Ohm/km				Ohm/km
Bakır İletkenler (Yuvarlak Kesitli)
1,5	12,1	15,4	0,0000	0,0000	1,0000	15,4
2,5	7,41	9,45	0,0000	0,0000	1,0000	9,45
4	4,61	5,88	0,0000	0,0000	1,0000	5,88
6	3,08	3,93	0,0000	0,0000	1,0000	3,93
10	1,83	2,33	0,0000	0,0000	1,0000	2,33
16	1,15	1,47	0,0000	0,0000	1,0000	1,47
25	0,724	0,923	0,0001	0,0000	1,0001	0,923
35	0,524	0,668	0,0002	0,0000	1,0002	0,668
50	0,387	0,493	0,0003	0,0001	1,0004	0,494
70	0,268	0,342	0,0007	0,0004	1,0011	0,342
95	0,193	0,246	0,0014	0,0017	1,0030	0,247
120	0,153	0,195	0,0022	0,0042	1,0063	0,196
150	0,124	0,158	0,0033	0,0096	1,0129	0,160
185	0,0991	0,1264	0,0051	0,0233	1,0285	0,1300
240	0,0754	0,0961	0,0088	0,0669	1,0757	0,1034
300	0,0601	0,0766	0,0138	0,1521	1,1660	0,0894
400	0,0470	0,0599	0,0225	0,3318	1,3543	0,0812
500	0,0366	0,0467	0,0367	0,6059	1,6425	0,0767
600	0,0283	0,0361	0,0601	0,9005	1,9606	0,0707
Alüminyum İletkenler (Yuvarlak Kesitli)
2,5	12,22	15,67	0,0000	0,0000	1,0000	15,67
4	7,64	9,80	0,0000	0,0000	1,0000	9,80
6	5,09	6,53	0,0000	0,0000	1,0000	6,53
10	3,06	3,92	0,0000	0,0000	1,0000	3,92
16	1,91	2,45	0,0000	0,0000	1,0000	2,44
25	1,20	1,54	0,0000	0,0000	1,0000	1,53
35	0,868	1,113	0,0001	0,0000	1,0001	1,107
50	0,641	0,822	0,0001	0,0000	1,0001	0,817
70	0,443	0,568	0,0003	0,0000	1,0003	0,565
95	0,320	0,410	0,0005	0,0001	1,0006	0,408
120	0,253	0,324	0,0008	0,0002	1,0010	0,323
150	0,206	0,264	0,0012	0,0005	1,0017	0,263
185	0,164	0,210	0,0019	0,0013	1,0032	0,210
240	0,125	0,160	0,0032	0,0038	1,0071	0,161
300	0,100	0,128	0,0050	0,0093	1,0144	0,129
400	0,0778	0,0997	0,0083	0,0251	1,0334	0,1025
500	0,0605	0,0776	0,0137	0,0661	1,0798	0,0833

Reaktans (X)

Alternatif akım, iletken üzerinde ister istemez bir manyetik alan ve elektrik alan oluşturacaktır. Bu alanların oluşması neticesinde kablo üzerinde endüktans ve kapasitans değerleri meydana gelir. Aslında bunların direk bir eneji kaybına yol açmaları söz konusu değildir ama manyetik ve elektrik alanların oluşması için kaynaktan bir miktar akım çekilmelidir. Bu akım I²R  kaybında küçük de olsa artışa sebep olur.

Kabloların endüktans ve kapasitans değerlerinden toplam reaktans değeri oluşur. Bu değer, kablonun tesis edildiği yer, yakınındaki çelik konstrüksiyon, başka kablolara komşuluk gibi bir takım büyüklüklere göre değişir. Ancak her zaman bu detatylara göre hassas hesaplama yapılamayacağı için çeşitli kaynaklarda verilen kablo reaktans değerlerinden yola çıkılarak hesaplamalara devam edilir.

Aşağıdaki tabloda bazı kabloların yerleşim tiplerine göre reaktans değerleri verilmiştir. (Tablo-3)

Kesit	Reaktans	Reaktans	Reaktans
	Ohm/km	Ohm/km	Ohm/km
mm2	TİP1	TİP2	TİP3
1,5	0,1150	0,2150	0,1484
2,5	0,1068	0,1997	0,1378
4	0,1065	0,1991	0,1374
6	0,1008	0,1886	0,1301
10	0,0946	0,1768	0,1220
16	0,0895	0,1681	0,1166
25	0,0861	0,1615	0,1100
35	0,0820	0,1561	0,1046
50	0,0826	0,1536	0,1021
70	0,0798	0,1486	0,0971
95	0,0795	0,1464	0,0949
120	0,0785	0,1439	0,0924
150	0,0776	0,1426	0,0911
185	0,0779	0,1417	0,0902
240	0,0770	0,1398	0,0883
300	—	0,1370	0,0865
400	—	0,1343	0,0848
TİP1	Aynı dış kılıf içinde Bakır iletken 3+1 damarlı kablo
TİP2	Tek damarlı bakır iletkenli kablolar
	3 adedi yanyana yatay düzlemde yerleştirilmiş
TİP3	Tek damarlı bakır iletkenli kablolar
	3 adedi üçgen formda yerleştirilmiş

 

Böylece gerilim düşümü hesaplarımızı yapmamıza sebep olan hat direnci (R) ve hat reaktansı (X) değerlerine nasıl ulaşacağımızı görmüş olduk.  Şimdi gerilim düşümü formülümüzü bir fazlı devreler ve üç fazlı devreler özelinde tekrar gözden geçirelim.

Bir fazlı devrelerde gerilim düşümü

Hesaba konu kablonun metre başına R ve X değerlerini  yukarıda verilen tablolardan aldıktan sonra iletken uzunluğu ile çarparak kablonun toplam R ve X değerleri bulunur.  Bundan sonrası formülde ilgili değerleri yerine konarak bulunur. (R için alternatif akım direncini kullanmayı lütfen atlamayalım, benzer şekilde X değerini de tablodan kablo yerleşim tipine göre almalıyız.)

Ancak şunu vurgulayalım, bir fazlı devrelerin gerilim düşümü hesaplarında nötr hattının empedansının da toplam kablo empedansına eklenmesi gerekmektedir. Bu sebeple L uzunluğunun yani pano ile tüketeç arasındaki uzunluğun 2 katını almamız gerekir.

Böylece bir fazlı devrelerdeki gerilim düşümü formülümüz şu hale gelmiş olur:

 

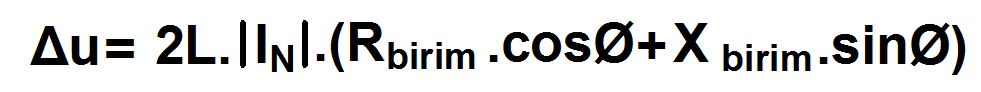
Üç fazlı devrelerde gerilim düşümü

Üç fazlı devrelerde, şayet dengeli yük varsa nötr hattından bir akım geçmez. Böylece nötr hattında bir gerilim düşümü olamaz ve haliyle sadece faz iletkeninin empedansı hesaba katılır. Yani bir fazlı devrelerde yaptığımız gibi uzunluğu 2 ile çarpmayız. Sadece pano ile tüketeç arasındaki uzunluk kullanılır. İlgili tablolardan metre başına R ve X değerleri alınıp hat uzunluğu L ile çarpılarak hattın toplam R ve X değerleri tespit edilir. (R için alternatif akım direncini kullanmayı lütfen atlamayalım, benzer şekilde X değerini de tablodan kablo yerleşim tipine göre almalıyız.)

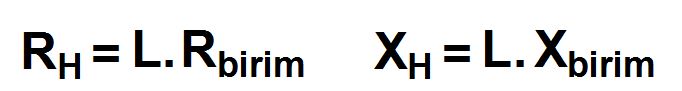
Üç fazlı sistemlerd gerilim fazarası değeriyle anıldığı için gerilim düşümü değerini de fazarası değere dönüştürmek adına √3 katsayısını da eklersek dengeli üç fazlı devrelerdeki gerilim düşümü formülümüz şu hale gelmiş olur:

 

Gerilim düşümü ile ilgili örnekler

 

Yukarıdaki 3 fazlı, 400V dengeli olarak çalışan bir tali pano beslemesi gösterilmiştir. Bu panoyu besleyen kablo üzerindeki gerilim düşümünü bulalım.

Kullanacağımız gerilim düşümü formülü, 3 fazlı dengeli sistemler için bulduğumuz aşağıdaki formül olacak.

Bu bağlantıda geçen kablonun birim uzunluk başına R ve X değerlerini tespit edelim.  Kablomuz N2XH tipinde olduğundan malzemesi bakır ve işletme sıcaklığı 90ºC dir.  70mm2 bakır için Tablo 2’den  alternatif akım direncini R=0,342 ohm/km olarak alırız. Ayrıca kablomuz 3+1 formunda olduğundan yani Tablo-3 e göre Tip-1 olduğundan Tablo-3 den X=0,0798 ohm/km değerini alırız.

sin(acos(0,8)) bağıntısını kullanarak sinØ=0,6 buluruz.

Son olarak P= √3 Un. In. cosØ bağıntısını kullanarak In=125000 / 400 / 0,8 /√3 = 225,53A değerini buluruz.

Bundan sonra değerleri gerilim düşümü formülümüze yerleştirelim.

dU= √3 . 100 . 225,53 . (0,342 . 0,8 /1000+ 0,0798 . 0,6/1000) = 12,55 V

e= dU/Un = 12,55/400 = %3,13

olarak bulunur.

 

Sonuç:

Lütfen, internet ortamında dolaşan ve aşağıda resmini verdiğimiz EMOnun eski usul hesap yöntemini kullanmamanızı öneririm. Eğer bu eski yöntemler gerilim düşümü hesabı yapsaydık, yukarıdaki örneğimizde sonuç e=%2,21 çıkacaktı. Yani %34 hatalı olacaktı.

Gerilim düşümü hesapları bir miktar hata payı içermektedir. Ama bu hata payı pratikte çok ufak olduğundan gözardı edilmektedir. Fakat sadece DC direnç değerlerini kullanarak gerilim düşümü hesabı yapmaktansa yukarıda detayını verdiğimiz şekilde kablonun AC direnç değerleri ve reaktansını kullanarak hesap yapmak daha doğru sonuçlar verir.

Tekrarlamak gerekirse tesisatlarda aranacak gerilim düşümü sınırı: Yapı bağlantı kutusu ile tüketim araçları arasında, aydınlatma ve priz devreleri için % l,5’i, motor devreler için % 3 ‘ü, geçmemelidir. Kendi trafosu bulunan tesislerde toplam gerilim düşümü, aydınlatma ve priz devreleri için %6,5, motor devreleri için %8 olabilir.

 

Bu linke tıklayarak, gerilim düşümü hesaplaması yapan online elektronik tablomuza ulaşabilirsiniz.

 

 

Kaynaklar:

İsa İlisu, TMMOB ELEKTRİK MÜHENDİSLERİ ODASI İSTANBUL ŞUBESİ BÜLTENİ Şubat 2016

IEC 60287-1-1 Part1-1

https://pdhonline.com/courses/e426/e426content.pdf